Skip to main content
Interactive Mathematics
Search IntMath
Close

IntMath Newsletter: Series interactives, Valentine’s heart

By Murray Bourne, 14 Feb 2017

14 Feb 2017

In this Newsletter:

1. Taylor, Maclaurin & Binary Series interactive applets
2. Math art: Valentine's heart
3. Math in the news
4. Math movie: Map of Mathematics
5. Math puzzles
6. Final thought: Essential fluids

1. Taylor, Maclaurin & Binary Series interactive applets

Taylor Maclaurin Series interactive applet

I recently added some new applets that help you explore approximations to various trigonometric and logarithmic functions using infinite series.

Taylor and Maclaurin Series interactive applet

Binomial Series interactive applet

These series expansions were incredibly useful when they were first developed by Newton, Taylor and Maclaurin in the 17th and 18th centuries, for their many uses in evaluating function values and in calculus.

Here's some background information so you know what's going on in the above applets:

Taylor Series and Maclaurin Series

The Binomial Theorem

2. Math art: Valentine's heart

Yes, it's that time of year again.

There are several ways to draw mathematical hearts. I quite like this one because it uses parametric equations, which are easier to deal with than implicit functions.

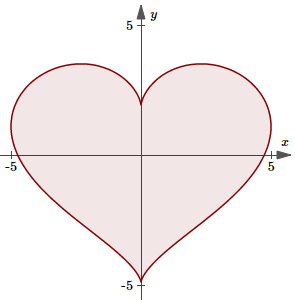
mathematical valentines heart
Mathematical Valentine's heart
x = 5 sin3(t),
y = 4 cos(t) − 1.3 cos(2t) − 0.6 cos(3t) − 0.2 cos(4t)

It's even simpler when you use polar equations.

You can see more parametric curves involving trigonometric functions here: Lissajous Figures

Happy Valentine's!

3. Math in the news

Here's some interesting recent stories involving math.

1. Lethal dose of caffeine given to students in university experiment

The court was told about a catalogue of errors that led to the overdose, which included the calculation being done on a mobile phone, the decimal point being put in the wrong place and there being no risk assessment for the test.

2. Taking graphics cards beyond gaming

The NVIDIA GPU (graphics processing unit) in your computer is making it possible to solve "systems of multiple simultaneous equations involving thousands to millions of variables" by making use of better and cheaper energy efficiency rather than memory.

3. Random numbers discovery improves climate simulations

"Small-scale ocean currents are fiendishly difficult to recreate in models, but we found that random numbers do a good job of standing in for them. This approach leads to significant improvements in our climate modelling abilities."

[Hat-tip to PiPo for the above stories.]

4. Math movie: Map of Mathematics

Map of mathematics

A lot of people form a narrow view of mathematics from their school experiences. This Map of Mathematics video by Dominic Walliman attempts to give a broad outline of the different fields of math.

See The Map of Mathematics

Here's a still image of the complete map (440 kB)

And here's a huge version that's clearer (770 kB)

By Dominic's own admission, there are 3 errors in the map. Can you spot them?

5. Math puzzles

The puzzle in the last IntMath Newsletter asked about the number of terms in a geometric sequence.

Correct answers with sufficient explanation were provided by Adeyemi, Aksel, Tomas, Don, and Eamon. (Honourable mention to Gerard who was very close.)

New math puzzle: Box

A square piece of metal is made into an open box by cutting a square with side s from each corner and turning up the sides. If the volume of the resulting box is v cm3, what are the dimensions of the original sheet of metal?

Bonus: If we needed to make a closed box out of the same piece of metal, what would its maximum volume be?

You can leave your responses here.

6. Final thought: Essential fluids

When I was in northern India recently, visibility on each smoggy morning was often only a few meters. I was reminded of what ocean explorer Jacques Cousteau once said:

Water and air, the two essential fluids on which all life depends, have become global garbage cans. [Jacques Yves Cousteau]

Until next time, enjoy whatever you learn.

See the 11 Comments below.

Related posts:

  1. Infinite series background Infinite series have played an important role in the development of mathematics, especially calculus....
  2. IntMath Newsletter: 3-D conics, interactives, March math In this Newsletter: 1. Interactive 3-D conic sections graph 2. List of math interactives on...
  3. IntMath Newsletter: Math carnival, new interactives, graphing letters In this Newsletter: 1. Carnival of Mathematics #114 2. Updated Graphs of tan, cot, sec...
  4. IntMath Newsletter: Series, clock, Simpsons In this Newsletter: 1. New on IntMath: Infinite series, Spinning clock 2. Resources: Simpsons math,...
  5. List of math interactives on IntMath.com Some background on the list of math manipulatives on IntMath.com...

Posted in Intmath Newsletters category - 14 Feb 2017 [Permalink]

Tags: ,

11 Comments on “IntMath Newsletter: Series interactives, Valentine’s heart”

  1. Bruno Bonvini says:
    14 Feb 2017 at 6:10 pm [Comment permalink]

    I have the following puzzle:

    X + 1/x = 5

    Solve for: (-b+/- SQR(25 - 4))/2 = (5+/-SQR 21)/2

    X**2 + 1/X**2 = ? And ?????

    Then I did :

    X*X + 1/X * X = 5*X

    X**2 + 1 -5*X = 0

  2. Chris Buchanan says:
    14 Feb 2017 at 7:57 pm [Comment permalink]

    Area of metal piece:
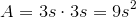
    {A}={3}{s}\cdot{3}{s}={9}{s}^{2}
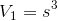
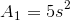
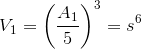
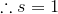
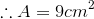
    Volume of open box:
    {V}_{1}={s}^{3}
    But the volume is made with 5 sides
    {A}_{1}={5}{s}^{2}
    {V}_{1}={{\left(\frac{{A}_{1}}{5}\right)}}^{3}={s}^{6}
    \therefore{s}={1}
    \therefore{A}={9}{c}{m}^{2}

    Max volume of closed box with same piece of metal:
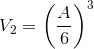
    {V}_{2}={{\left(\frac{A}{6}\right)}}^{3}
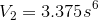
    {V}_{2}={3.375}{s}^{6}
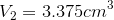
    {V}_{2}={3.375}{c}{m}^{3}

  3. Basil Norburry says:
    15 Feb 2017 at 12:02 am [Comment permalink]

    square metal has length 2s +sqrt(v/s)
    Max vol =4s^3

  4. Don A says:
    15 Feb 2017 at 1:27 am [Comment permalink]

    Let length of the side of the metal square be=L

    Area of base 'B = (L-2s)^2', Height is s

    So, 'V=B*H=((L-2s)^2)s'

    Solving for 'L=(sqrt(V/s))+2s' If V is cm^3 and s is cm then L is cm.

  5. Bharat says:
    16 Feb 2017 at 5:59 am [Comment permalink]

    What are the dimensions of the original sheet of metal?

    2s + sqrt(v/s)

  6. don miller says:
    16 Feb 2017 at 4:18 pm [Comment permalink]

    PART I
    Let s^2 be removed corner and x be length of side of square under study. V = volume of the "open box"...sides folded up after 4 corner squares removed. Area with corners in place is
    (1) x^2 = (x-2s)^2 +4{s^2 +(x-2s)s}.

    Mult by s
    (2) sx^2 = s(x-2s)^2 +4s{s^2 + (x-2s)s}

    Next, sub V for the first term in (2) and divide by s
    (2a) x^2 = V/s +4s^2 +4xs - 8s^2

    Re arrange (2a) into quadratic form
    (3) x^2 -4sx+{4s^2 -V/s} = 0

    Solving for x

    x = 2s +sqr(V/s) ANSWER PART I

    PART 2

    The top of a closed box must have the same area as the bottom. The area is (x-2s)^2

    Here we have 4s^2 left over from the open box case. Since the closed box top has the same area as the bottom, we will look for the value of s such that

    4s^2 = (x-2s)^2
    = x^2 -4xs +4s^2
    x^2 = 4xs
    s= x/4

    Max Vol (part 2) is x cube/16
    Then V ={x-2(x/4)}^2 *(x/4) = xcube/16

    Although not proven here, since all of x^2 metal has been used and the box is closed, we have a max volume closed box.

    Note: Part II solution assumes that the 4 corner pieces can be used as "one top" equal in area to the bottom.

  7. jeel says:
    17 Feb 2017 at 5:29 pm [Comment permalink]

    l=length of side of original square
    Then
    sx(l-2s)^2=v
    Then
    l=sqrtroot(v/s) +2s

  8. Yousif Taha says:
    23 Feb 2017 at 1:19 pm [Comment permalink]

    Let x be the side of cut corner square
    0 < x < s/2
    V= (s-2x)^2*x
    V= s^2x-8sx+12x^2
    V'= s^2-8sx+12x^2
    s^2-8sx+12x^2=0
    6x=s , 2x=s
    x=s/6 , x=s/2
    Original side of square = 2s/3

    V= (s-s/3)^2*s/6
    V= 2s^3/9

  9. Saikrishna Nadella says:
    12 Mar 2017 at 9:43 pm [Comment permalink]

    Dear sir,
    Answer for the puzzle is:
    Dimensions of sheet are 3sx3s.
    Max volume of closed box with same sheet is 27/(16√2) s^3 = 1.1932 v

    Explanation:
    1) procedure for making open boxes is mentioned as "cutting squares at corners". So, square cut at corner of square sheet means, the final box side is also "s".
    So, side of square sheet is 3s
    2) for making closed box with maximum volume, we can cut isosceles triangles of side a at the center of each edge of the square sheet such that 3s=2√2 a. Then the remaining part can be folded into a cubic closed box. The traingualar corners of sheet becomes closing flaps of the box. Excuse me for not able to attach a picture. Then volume will be (a^3)=(3/(2√2)s)^3 = 1.1932v

  10. Jatin says:
    16 Mar 2017 at 9:30 pm [Comment permalink]

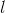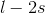    Let the side length of the metal piece be l. After removing squares of side s from all corners and folding up the sides to make an open box the edge length of open box would be l-2s. So volume of box would be 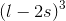(l - 2s)^3 which is same as v.So,
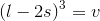
    (l - 2s)^3 = v
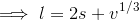
    \implies l = 2s + v ^{1/3}
    which will be the dimension of the metal sheet.

  11. Murray says:
    25 Mar 2017 at 10:24 am [Comment permalink]

    @Bruno: Please ask your math questions on the IntMath Forum. Here's the appropriate section: Quadratic Equations.

Leave a comment




Comment Preview

HTML: You can use simple tags like <b>, <a href="...">, etc.

To enter math, you can can either:

  1. Use simple calculator-like input in the following format (surround your math in backticks, or qq on tablet or phone):
    `a^2 = sqrt(b^2 + c^2)`
    (See more on ASCIIMath syntax); or
  2. Use simple LaTeX in the following format. Surround your math with \( and \).
    \( \int g dx = \sqrt{\frac{a}{b}} \)
    (This is standard simple LaTeX.)

NOTE: You can mix both types of math entry in your comment.

top

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.