IntMath Newsletter: Solid of revolution, resources, news
By Murray Bourne, 10 Oct 2018
10 Oct 2018
In this Newsletter:
1. New on IntMath: Solid of Revolution maker
2. Resources: Grasshopper, Sketchup
3. Math in the news: Light beam
4. Math movies: Ballet, Mars
5. Math puzzle: Tokens
6. Final thought: Jack Ma
0. Happy Metric Day!
Today is 10/10 and this week is designated National Metric Week. Of course, this is probably only relevant in the USA only, as every other country in the world officially uses metric units (except Myanmar). The US Metric Association advocates completion of the ongoing US conversion to the metric system.
1. New on IntMath
Math Art in Code: Solid of Revolution maker
 |
Create your own solid of revolution using this interactive 3-D graph. Drag across the canvas and the shape automatically appears. |
2. Resources
(a) Grasshopper
 |
Learn to code using the Grasshopper game for Android and iOS devices. It's by Google, and it teaches you javascript basics in a fun and painless way. Go to: Grasshopper codes |
(b) Sketchup Viewer is now free
Sketchup is a 3-D modeliing software for desktops. The "core" version comes at zero cost, with education and Pro versions also available.
They recently provided Sketchup Viewer for iOS and Android devices, so you can view the thousands of models made using Sketchup for $0.
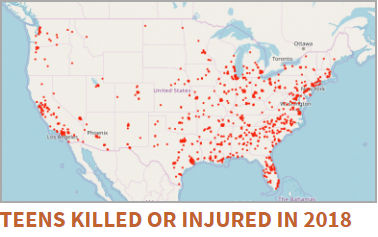
(c) Gun violence data visualizations
On average in the USA there are around 10 teenagers killed by guns each day. I've lived my whole life in countries where guns are illegal, and I'm yet to understand how any country can allow such violence to continue.
For a sobering set of visual statistics, see the Gun Violence Archive.
3. Math in the news
(a) Needle pulse light beam
Obtaining precise images is extremely important in many fields of science, engineering and medicine. Ultrasound, radar and precise metal etching are notable applications.
 |
Researchers at University of Rochester used a mathematical approach to cause a light or sound wave to collapse inward, forming a short duration, incredibly thin intense beam, which they call a "needle pulse" beam. Here's an overview: New 'needle pulse' beam pattern packs a punch |
Here's the original paper, containing all the juicy mathematics involved:
Longitudinal iso-phase condition and needle pulses (link no longer exists)
(b) Teaching for understanding?
Sadly, far too many students think of mathematics as a series of formulas that just require subsituting a number or two, getting it right (hopefully), and moving on to the next one.
 |
But what is mathematics really about and how should it really be taught? See: Challenging the status quo in mathematics: Teaching for understanding |
4. Math Movies
(a) The physics of the "hardest move" in ballet
In the third act of "Swan Lake", the Black Swan spins around and around ... thirty-two times.
 |
How is this move — which is called a fouetté — even possible? Arleen Sugano unravels the physics of this famous ballet move. |
(b) What time is it on Mars?
We often feel everyone else has the same experience of time as we do. But what if you were on Mars? Or at least, your job required you to study Mars? This video does a good job of challenging our perspective.
 |
As a spacecraft engineer at NASA's Jet Propulsion Laboratory, Nagin Cox works on the team that manages the United States' rovers on Mars, whose day is 40 minutes longer than Earth's. |
5. Math puzzles
The puzzle in the last IntMath Newsletter asked about dividing factorial numbers. Correct answers were submitted by Gerard, Francis, Aaron, and Rajat.
New math puzzle: Tokens
I have tokens labelled 1, 2, 3, ... and ten boxes labelled 1 to 10. In the first box I place the first token, in the second box the next two tokens, in the third box, the next three tokens, and so on. What is the sum of the numbers on the tokens I place in the tenth box?
You can leave your response here.
6. Final thought - Jack Ma and teaching
Chinese billionaire Jack Ma is stepping down from Alibaba to pursue philanthropy in education. He will follow in Bill Gates' footsteps, putting his fortune to good use. Here are two recent quotes which I found interesting, especially as teaching is not always given the respect it deserves.
"I also want to return to education, which excites me with so much blessing because this is what I love to do." [Source]
Here's an indication of how he intends to approach education given his experiences. It will be interesting to see what innovative things he does.
"I'm not going to teach you math. I'm not going to teach you English. I'm not going to teach business in the schools. I'm going to teach young people how to face challenges." [Source]
Until next time, enjoy whatever you learn.
See the 13 Comments below.

10 Oct 2018 at 10:42 pm [Comment permalink]
Well, I didn't do any fancy math. In fact, I just used a spreadsheet and "put" tokens into "buckets". I came up with 505 for the sum of the tokens in the 10th "bucket". I would really like to learn the math behind this. I would imagine factorials are involved, but I imagine it is pretty tricky.
11 Oct 2018 at 1:39 am [Comment permalink]
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 +10
= (First + Last)x10÷2 = 55
11 Oct 2018 at 3:02 am [Comment permalink]
Not sure if this is for students only, but I'll answer anyway.
The total number of tokens placed in bins 1-9 = sum of the natural numbers from 1 to 9 = (9/2)(1+9) = 45. Forty-five is also the value of the last token placed in bin 9. Therefore bin 10 gets ten tokens of increasing unit value starting with a value of 46. Thus the total value of all tokens in bin 10 = (10/2)(46+55) = 505.
11 Oct 2018 at 4:27 am [Comment permalink]
1+2+3+4+5+6+7+8+9=(1+9)*(9/2)=10*4.5=45
46+47++48+49+50+51+52+53+54+55=(46+55)*(10/2)=101*5=505
505
11 Oct 2018 at 5:56 am [Comment permalink]
I believe the sum of the tokens placed in the 10th box is 505.
11 Oct 2018 at 3:14 pm [Comment permalink]
In the tenth bag the token number 46-55 placed, their sum will be 505.
12 Oct 2018 at 2:07 am [Comment permalink]
Shouldn't the last word in the puzzle be "box", not "bag"?
Anyway, the general formula for the sum of the tokens in the nth box would seem to be: n(n+1)/2 + n^2(n-1)/2. If n is 10, this evaluates to:
55 + 450 = 505.
Doug Gerrard
12 Oct 2018 at 4:32 am [Comment permalink]
One more thought: The solution to this problem which I submitted earlier today can be further simplified to: n(n^2 + 1)/2, a result analogous in form to that for the sum of the first n integers.
12 Oct 2018 at 6:25 am [Comment permalink]
I believe the answer is 505. At the end of the 9th box, you have used the first 45 natural numbers. Then we have to get the summation of the next 10 natural numbers, starting from 46. We can use the summation of arithmetic series where n = 10 and the initial number as 46 with the common difference as 1.
12 Oct 2018 at 8:47 am [Comment permalink]
In the first 9 boxes, how many tokens are there? 1 + 2 + 3 +...+ 9
Using the standard approach, we find there are 45 tokens. These are numbered from 1 to 45.
In the tenth box, there are 10 tokens which must be numbered from 46 to 55. We can apply the formula for the sum from 1 to 55 and subtract the sum from 1 to 45 or apply the same logic to these 10 numbers alone. 46 + 55 = 101...50 + 51 = 101, there are 5 sets so the sum is 5 * 101 = 505
15 Oct 2018 at 11:30 pm [Comment permalink]
I start by considering a sequence of tokens 1, 2, 3,... and split this sequence into bins of increasing size, i.e., (1), (2, 3), (4,5,6), (7,8,9,10),... Notice that the last elements of each of the bins form the sequence (1,3,6,10,... ). With this in mind, it is easy to use elementary list operations in Mathematica to produce the sequence of sums of the consecutive bins. Then, the first ten elements of the sequence of sums are (1, 5, 15, 34, 65, 111, 175, 260, 369, 505), so that the answer is 505.
26 Oct 2018 at 10:23 pm [Comment permalink]
The number of tokens is 220, obtained as follows.
We need the sum S=1+(1+2)+(1+2+3)+....+(1+2+3+...+10)
To simplify the problem, suppose initially we had just 4 boxes.
Then S=1+(1+2)+(1+2+3)+(1+2+3+4)
We could also write this sum as:
S=1+(2+1)+(3+2+1)+(4+3+2+1)
or again as:
S=4+(3+3)+(2+2+2)+(1+1+1+1)
Adding these three forms vertically we obtain:
3S=6+(6+6)+(6+6+6)+(6+6+6+6) = 6(1+2+3+4)
Extending the principle to 10 boxes it is clear that we would obtain:
3S=12(1+2+3+...+10) = 12x55 = 660, hence S=220
Addendum: since 1+2+3+...+n = n(n+1)/2, we can write a general solution for the number of tokens in n boxes as 3S=(n+2)(n)(n+1)/2, hence S=n(n+1)(n+2)/6
For n=10, S=(10x11x12)/6 = 10x11x2 = 220
28 Nov 2018 at 11:13 pm [Comment permalink]
505