How do you find exact values for the sine of all angles?
By Murray Bourne, 23 Jun 2011
Challenge: What is the exact value for sine of 6 degrees? How about sine of 1 degree?
Context: I received a delightful email from reader James Parent recently. He wrote:
I have the exact answers for the sin of all integer angles. Has anyone done this before? I'm retired, and a Professor Emeritus from a community college. I'm 74 years-old.
This certainly sounded interesting to me, so I asked James to write a guest post, and here it is. (Many of James' mails had the tag-line "Sent from my iPad".)
Over to James.
How do you find exact values for the sine of integer angles?
Here is one way of going about it.
Background
Let’s find some exact values using some well-known triangles. Then we’ll use these exact values to answer the above challenges.
sin 45°: You may recall that an isosceles right triangle with sides of 1 and with hypotenuse of square root of 2 will give you the sine of 45 degrees as half the square root of 2.
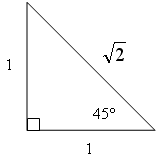
sin 30° and sin 60°: An equilateral triangle has all angles measuring 60 degrees and all three sides are equal. For convenience, we choose each side to be length 2. When you bisect an angle, you get 30 degrees and the side opposite is 1/2 of 2, which gives you 1. Using that right triangle, you get exact answers for sine of 30°, and sin 60° which are 1/2 and the square root of 3 over 2 respectively.
Using these results – sine 15°
How do you find the value of the sine of 15°?
Sine of half an angle in the first quadrant is given by the expression:
So the sine of 1/2 of 30° will be:
which gives us
or
Note: We could also find the sine of 15 degrees using sine (45° − 30°).
sin 75°: Now using the formula for the sine of the sum of 2 angles,
sin(A + B) = sin A cos B + cos A sin B,
we can find the sine of (45° + 30°) to give sine of 75 degrees.
We now find the sine of 36°, by first finding the cos of 36°.
cos 36°: The cosine of 36 degrees can be calculated by using a pentagon. See cos36° at CutTheKnot where it is shown that
Putting these values on a right triangle and solving for the unknown side, we can conclude:
sin 18°: Now, the sine of 18 degrees comes from the sine of half of 36 degrees.
Calculating this, the sine of 18 degrees becomes
sin 3°: The above leads you to one of the paths to sine of 3 degrees and to sine of 6 degrees.
For example, sine (18° - 15°) will give us the sine of 3 degrees. which is
sin 3° = sin (18° − 15°) = sin 18° cos 15° − sin 15° cos 18°
This gives us the following value of sin 3°:
or other forms depending how you factor the above.
sin 6°: Using the above, one can compute the sine of 6 degrees finally as sine of twice 3 degrees to arrive at
sin 18° and sin 72°: Taking the equivalent sine and cosine values of 15° and 18° on the right hand side of
sin 3° = sin (18° − 15°) = sin 18° cos 15° − sin 15° cos 18°
gives us:
sin 3° = sin 18° sin 75° − sin 15° sin 72°
We can calculate the values of the sines of 18° and 72° from the above expression.
Sines of other angles
Many angles can be computed exactly by many methods. Another practical formula is the sine of 3 times an angle:
sin 3A = 3 sin A − 4 sin3A
sin 9°: For example, the sine of 9 degrees is the sine of (3×3°).
So, with A = 3, we arrive at
And so on.
sin 1°: Now, to find the sine of one degree, one needs to know sine of one third of three degrees!
One needs to solve the above for sin (A) in terms of 3A, and this involves solving the cubic. As you know, the cubic was solved many, many years ago.
There are three solutions and one needs to know which one to use and when! Experience has taught me to use the following for a quadrant I angle (the "I" in this expression stands for the imaginary number √(−1). See Complex Numbers for more information.)
[Click image to see full size]
Use the following when you have a quadrant II angle:
Use the following for quadrant III angles:
[Click image to see full size]
So, the expression for sine(1°) becomes
[Click image to see full size]
Messy, isn't it! But, it does give you the exact value for the sine of one degree.
Is it correct?
Evaluate the sine of 1 degree using a TI Scientific Calculator and you will get 0.0174524064. Evaluate the above messy expression and you will also get 0.0174524064. Even allowing for calculator rounding errors, we can be confident our answer is correct.
List of all sines of integer degrees from 1° to 90°
This PDF contains all the exact values of the sine values for whole-numbered angles (in degrees):
Exact values sin 1° to sin 90° [PDF, 293 kB]
Concluding Comments from James
For a retired community college mathematics professor since 1997, this has been a lot of enjoyment for me.
James Parent, Professor Emeritus
Schenectady County Community College, Schenectady, New York
Currently teaching as an adjunct at Great Bay Community College, Portsmouth, New Hampshire
Alternative List: sines and cosines of integer degrees from 3° to 90° (multiples of 3)
Reader Herwig Ronsmans wrote a comment to say he had found the sines and cosines of multiples of 3° (i.e. 3°, 6°, 9°, ...). He mentioned his list has simpler expressions for many of the angles compared to the above PDF.
He kindly shared his list: Sines and cosines of multiples of 3° [PDF, 165 kB].
It's in Dutch, but as Herwig said, mathematics is universal and so it's easy to work out what he's doing if you're not a Dutch speaker.
Simplifying Radicals
As pointed out by several commenters and readers, this solution is lengthy for the sake of completeness, but can be reduced in steps using the Simplest Radical Form.
See the 102 Comments below.
24 Jun 2011 at 5:56 pm [Comment permalink]
Unbelievable.
25 Jun 2011 at 1:02 am [Comment permalink]
An easy method to memorize the sequence sin(0°), sin(30°), sin(45°), sin(60°), sin(90°). Here is it:
1. Write below five division lines the digit 2:
2. Write the digits 0, 1, 2, 3, 4 at the top
3. Sqrt the top digits:
4. You are ready:
sin(0°) = 0
sin(30°) = 1/2
sin(45°) = √2/2
sin(60°) = √3/2
sin(90°) = 1
25 Jun 2011 at 9:48 am [Comment permalink]
Thanks, Philip! This one is new to me. We all have different ways of learning and understanding things.
I never try to memorize these exact values - I just sketch the diagrams quickly and read them from there.
30 Jun 2011 at 12:46 am [Comment permalink]
This is a nice piece of work and possibly quite engaging to some of our high school students taking Trig. My only critique is kind of nitpicking, but the title refers to "any" angle, while the professor clarifies later to any "integer" angle (in degrees). Until he cleared it up, my first thought was "What about irrational angles?
1 Jul 2011 at 3:01 am [Comment permalink]
This is wonderful! Easy remembrance of trig ratio of special angles INDEED !
2 Jul 2011 at 6:23 am [Comment permalink]
@Douglas: The title was already quite long, that's why the word "integral"was not included. Also, it made the piece look less palatable!
2 Jul 2011 at 1:25 pm [Comment permalink]
"integral" = "integer" ? 🙂
10 Jul 2011 at 4:26 pm [Comment permalink]
Certainly amused by the amount of detail it goes to. I hate remembering stuffs, and taking the extra mile to understand is totally worth it. I'm having a problem understanding how this formula works though.
Ok I know why the value of cos 30 is the square root of 3 over 2, but why the other stuffs around it?
11 Jul 2011 at 8:26 am [Comment permalink]
@Bonzoni: You can find an explanation for this and other "half angle" formulas here: Half angle formulas.
27 Jul 2011 at 7:01 am [Comment permalink]
Wow this is an amazing find. This list is certainly powerful using it one can easily calculate the cosine values because sine and cosine are cofunctions. Next tangent can be calculated via tan(x) = sin(x)/cos(x). Then getting the reciprocals is easy work. For any integral angle other than 1 through 90° you simply apply the quadrant rules. Very cool work.
3 Apr 2012 at 11:40 am [Comment permalink]
How do you solve cos36 degree without using a calculator ?
3 Apr 2012 at 3:34 pm [Comment permalink]
@Keng Keh. The answer is in the article, about 1/2 way down. There is a link which shows how to do it via a pentagon.
5 Apr 2012 at 9:46 am [Comment permalink]
Thank you Mr Murray, I got it !
27 Apr 2012 at 10:29 am [Comment permalink]
Thanks a lot !!!
Onto to my new Maple 16 and Mathematica 8.0.4 to calculate the values for cosine.
18 Jun 2012 at 5:00 pm [Comment permalink]
Why the value of sin30 is half?
19 Jun 2012 at 8:43 am [Comment permalink]
@Raj: This page has the answer
Values of Trig Functions
20 Jun 2012 at 3:07 am [Comment permalink]
how will give the value in bisection method cos1 value ?
9 Aug 2012 at 10:37 am [Comment permalink]
Thank very much for the work done by Professor James Parent, I note that there is one typing mistake for sin3A which should be equal to 3sinA - 4(sinA)^3
9 Aug 2012 at 10:49 am [Comment permalink]
@Hans - Thank you for spotting the error. I have amended the article.
21 Sep 2012 at 2:13 pm [Comment permalink]
Sorry to take up so much comment space. Please reply if you can add to this observation.
Mr. Bourne and Prof. Parent;
I worked for many years as a video shop and field technician and used complex waveforms on oscilloscopes to align machines, which drew somewhat on my math background from high school and early college. We used sine waves and lissajous figures, which were rather simplified on the graphic screen of the scopes. We didn't do that much calculation, as it were.
Much of that work has dried up and now I've gone back to brush up on my math skills and perhaps may even go back to school. While trying to regain my algebra, trigonometry, and calculus I started working on the unit circle, and working out the sine and cosine and tangent of the basic angles. I looked around on the internet for examples and found some great examples and interesting reading on your math page. I have something that I hope may be a worthwhile contribution to the pages.
I was intrigued by the project on your page where a Professor Emeritus James Parent showed how to derive the constant values for the sines of all integer angles, using various formulas and methods. I worked for a while to understand how he got 36 and 18. Then I went back and looked at 15 and 75, which are a bit easier to understand. While looking at his derivation of sine of angle 15 I noticed that he came up with an answer that didn't fit my calculation using the half angle rule.
In Professor Parent's commentary, he works out sine 15 using the half angle formula sq root ((1 - cos 30) / 2), and shows that it simplifies to 1/2 x sq root( 2 - (sq root 3)), which he says, quite nonchalantly "or", further simplifying the expression, to 1/4 x sq root 2 x (sq root 3 - 1).
The simplification, using algebra, to go from the first expression to the second, is quite tricky. I think he may have put in the second expression without any fanfare, since both quantities are used for the value of sine 15.
It's interesting that his solution to the problem of sin 15 leads to a way to denest the radical in the expression sq root (2 - (sq root 3)). Without going through the process of squaring, expanding, and using the quadratic formula as I've seen performed, you can use a kind of trigonometric substitution to get back to sin 15. Then you can solve for sin 15 with the difference formula, writing sin 15 = sin (45 - 30). Using the formula sin45 x cos 30 - cos45 x sin 30, you will come up with sq root (6) / 4 - sq root (2) / 4, which can be written as 1/4 x sq root 2 x (sq root 3 - 1), the Professor's end answer for sine 15.
If one were to start with a simple, commonly seen nested radical of sq root (2 - ( sq root 3)), you could multiply by 1/2, or 1/sq root 4, and that would get you to sq root ((2 - sq root 3) / 4). This can be rewritten as sq root ((1 - cos 30) / 2). This equals sin 15 by the half angle theorem. Now substitute sin 15 by the difference theorem, using sin (45 - 30). This will produce the denested answer 1/2 x sq root( 2 - (sq root 3)).
A similar trigonometric substitution can be used to denest (2 + ( sq root 3)), using cos 15, translating from the half angle formula of cos 30 and the difference formula of cos 45 - 30.
It works for angles 150 and 75, although you get the same answer values. I don't see any other substitution denest shortcuts very readily. It would be anywhere you could get an angle by the half angle formula, which often produces a nested radical, and get the same angle by a sum or difference formula. I'll look for others in the degrees and pi fractions.
Perhaps a similar manipulation can be done between the three times or one third formula, and a sum or difference of angles that have a product and sum in common.
What do you think of this method? Is this a known or often used substitution to simplify a nested radical? It seems no less magical slight of hand than going through the quadratic formula.
If you need to see a more completely written out form of the math I can send. It would be nice to do it in a format that has the radicals in a printed form so it's more clear.
-Keith J.
21 Sep 2012 at 8:44 pm [Comment permalink]
Hi Keith
Thanks for your inputs! Yes, some of the formulas could be simplified. Of course, at the end of the day the main point was to show that it can be done.
20 Nov 2012 at 3:51 pm [Comment permalink]
I'm impressed by your compilation of exact sine table. However, in the mission to derive the exact algebraic expression of sin(1°), we reach a difficult destination: a complicated form of radicals which contains the IOTA. If we try to remove it in order to get a cleaner IOTAless form, we have to apply deMoivre or binomial expansion, both of which lead to a form which is the sum of a sine series and a cosine series. Conclusion is that, we cannot achieve an algebraic expression of sin(1°) which contains only surds and rational numbers as we have for angles which are multiples of 3°.
My question is that, in such a situation, how can we say that sin(1°) is irrational when it appears to be a transcendental number? Just because 1° is a rational multiple of pi, should sin(1°) be declared irrational instead of transcendental?
27 Nov 2012 at 8:30 am [Comment permalink]
@Pinaki ROY 20 Nov 2012 at 3:51 pm,
See if this helps:
I remember vaguely that for nonzero x, both x and sin x cannot be algebraic. It might have been in S. Lang's Transcendental Numbers. (Here x of course is in radians). Irrational numbers are partitioned into algebraic and transcendental.
18 Dec 2012 at 11:54 pm [Comment permalink]
In fact, it is not the sin of 36, rather the cosine of 36 which is (1 + sqrt(5))/4
19 Dec 2012 at 9:02 am [Comment permalink]
Good catch, Marshall! Hmmm - If anyone has plenty of time, please let me know of any other problems with all these calculations and I'll tidy it all up in one go.
28 Dec 2012 at 1:31 am [Comment permalink]
Glad I could help... I teach at a university, mostly calculus 1 and 2....... I make up a very detailed key to my tests, including a detailed grading standard for awarding points..... never taking them away..... but the relevant remark is this: I think the last time I got a 100 on one of my own tests was sometime before the Civil War..... hehehe....keep up the good work!!!!
23 Jan 2013 at 12:27 pm [Comment permalink]
I am not certain the answer for sin(1) (I mean one degree) is correct. Your answer is of the form
where
This simplifies to
where
When you compute the cubic root of a number, you get three possibly complex answers. Therefore, your answer will result in the following:
with k=0,1,2.
There are two problems with this. First, none of them is cos(89) = sin(1). Second, even if you had cos(89) as one of the answers, all you would have shown is that sin(1)=cos(89)=sin(1), which is trivially true.
I believe the problem for all answers you have provided for angles that are not multiple of 3 degrees is that you have cubic roots of complex numbers in them. Those cubic roots will end up to be of the form re**(j*phi), and you'll end up showing sin(x) = sin(x).
Am i missing something here?
8 Feb 2013 at 3:03 pm [Comment permalink]
[...] Determining sine for all angles [...]
14 Apr 2013 at 1:36 am [Comment permalink]
This is a great list of exact values. Professor James Parent is a regular Ramanujan.
23 Apr 2013 at 4:51 pm [Comment permalink]
the answer equations in the form as provided by Nader Moayeri in 23.1.2013 are incorrect in both the answer equations and the expression for 'a', they are not the exact replica of the solution of sin(1 degree) as provided by James Parent. The solution by James making two complex roots adding togther may be misleading, the solution for cubic equation provided by T. Irvine in his website http://www.vibrationdata.com is good for reading.
25 Apr 2013 at 10:38 pm [Comment permalink]
Fantastic reading! I have a question about the second comment though - I too have used the method for "easy" exact values where you write the numbers 0-4, put each of them over 4 and take the square root, however I cannot find anywhere about where this comes from or why it works! Can anyone enlighten me? I don't like teaching things when I am unsure of their origin, even when I know it works!
26 Apr 2013 at 6:10 am [Comment permalink]
@Siobhan: Well, the origin is the ratios for the 30-60 and 45-45 triangles as mentioned in the article. From there, it's just an observation.
I think it's the same kind of question as "Why does a 3-4-5 triangle work to give us a right angled triangle?" It's just one observation of a specific case of Pythagoras' Theorem.
28 May 2013 at 9:14 am [Comment permalink]
I thank Hans Chan (see his post of April 23, 2013) for pointing out errors in what I had posted on January 23, 2013. This is an attempt to fix the errors and set the record straight.
The first expression in my earlier post was correct, but the expression for a was incorrect. Here's the correct version:
a = (1/24)(3)^(1/2)(3-(3)^(1/2))((5+(5)^(1/2))^(1/2))
- (1/48)(6)^(1/2)((5)^(1/2)-1)(3+(3)^(1/2)) = -0.052335956
and the correct value for theta is
theta = 93 degrees
When you compute the cubic root of e^(j theta) and e^(-j theta), each will have three cubic roots. This leads to nine possible combinations. Six of these will result in complex numbers as the answer for sin(1 degree), which is obviously unacceptable. Three will result in real numbers and turn out to be cos(89 degrees), cos(31 degrees), and cos(29 degrees). Obviously, the last two are wrong answers. The correct answer is sin(1 degree) = cos(89 degrees), but this is trivially true.
The problem comes from the fact that Professor Parent's expression for sin(1), albeit mathematically correct, requires computation of cubic roots of two complex numbers. I do not know of any way of computing the n'th root of a nonzero complex number other than converting the complex number to the form rho e^(j theta), where rho > 0 and 0 <= theta < 2 pi, and then writing the roots (there will be n of them) as
(rho)^(1/n) e^(j(theta + 2k pi)/n); k= 0, 1, ..., n-1
but the expression for theta includes an inverse tangent function. So, the only way I know how to compute the expression given by Professor Parent for sin(1) is to hit that tan^(-1) key on the calculator and then I would need to hit the cos key also, because the final answer will be of the form of cosine of some angle, 89 degrees to be specific.
If any of you know how to compute the cubic root of a complex number without using an inverse trigonometric function, please let the rest of us know. If such a procedure does not exist, then it would be reasonable to conclude that the expression given for sin(1) is just a mathematical curiosity, because it cannot be computed without invoking inverse trigonometric and trigonometric functions. The whole point of Professor Parent's work was to find expressions for sin of integrer-valued (in degrees) angles using the four basic arithmetic functions (+, -, *, and /) and square and possibly cubic roots of real numbers. Otherwise, to compute sin(1), all you have to do is hit the 1 button on your calculator followed by the sin button.
28 May 2013 at 9:39 am [Comment permalink]
Perhaps the following would be of interest to this group. I derived the following formulas. I am sure these must be known. SO, I suspect I have reinvented the wheel!
Anyway, this is about finding the square roots of the complex number a+jb. The answer is plus minus (I don't know how to do this without causing confusion)
(((a^2+b^2)^(1/2)+a)/2)^(1/2) + j (((a^2+b^2)^(1/2)-a)/2)^(1/2)
if b >=0, and plus minus (because each complex number has two square roots)
(((a^2+b^2)^(1/2)+a)/2)^(1/2) - j (((a^2+b^2)^(1/2)-a)/2)^(1/2)
if b < 0.
The point is that you can find the square root of a complex number of the form a+jb directly and without the ned to use trigonometric and inverse trigonometric functions.
I tried hard to derive similar expressions for the cubic root of a+jb, but all my attempts failed. In the 2-3 approaches I pursued, eventually the trigonometric and inverse trigonometric functions crept in as a result of the need to solve a cubic equation.
Well, for what it's worth I decided to share the above with you, just in case you have not seen it.
29 May 2013 at 9:18 am [Comment permalink]
Nader Moayeri has pointed out the puzzle that cubic root of complex number may not generate the meaningful result as wanted. I thank for his work to find sensible answer. However complex number is a field out of real number, so its geometric interpretion is uneasy to be visualized.
1 Jun 2013 at 12:09 pm [Comment permalink]
I am afraid I do not understand what Hans Chan is saying in his May 29, 2013 post. This has nothing to do with one or more choices for the two cubic roots that have appeared in Professor Parent's expression for sin(1) resulting in wrong answers. In many physical problems you solve an equation and you discard some of the roots because they are not acceptable. What matters is that one set of choices for the two cubic roots results in a value of cos(89) = sin(1) for the expression provided by Professor Parent, and that is obviously the right answer.
This has nothing to do with geometric interpretation of complex numbers either. We are really not looking for a geometric interpretation.
What matters is that Professor Parent's goal was to derive an expression for sin(1) whose computation requires only the four basic arithmetic operations and square roots (see the expressions he has provided for sin(45), sin(30), sin(60), sin(75), sin(15), sin(36), sin(18), sin(3), sin(6), and sin(72)). However, I maintain that the computation of the expression he has provided for sin(1) involves using an inverse trigonometric function followed by a sin or cos (trigonometric functions). So, Professor Parent's expression for sin(1) is of a different nature than the expressions he has provided for all those other angles just listed. It does not meet the requirement of needing only +, -, *, /, and square roots. If someone can find an expression for sin(1) that meets that condition, then I would say he/she has solved the problem. (p.s. A Taylor series expansion is not acceptable!) Until then, the problem remains unsolved.
24 Oct 2014 at 11:04 am [Comment permalink]
Dear James Parent: This was extremely helpful to me! Thank you so much for taking the time to post it. LLAP 🙂
1 Nov 2014 at 2:18 am [Comment permalink]
Sine 36 value is WRONG
Actually COS 36 is what you put in place of SINE 36
1 Nov 2014 at 2:30 am [Comment permalink]
Hi All,
Sorry for being so abrupt in my previous comment.
I went through derivation given in the link and when I came back sin 36 seemed to have a value for cos 36.
cos 36° = (√5+1)/4
Sin 36 = sqrt(2(5−√5))*(1/4)
sin 18 = (−1+√5)/4
So please look into it.
Regards
RJ
18 Nov 2014 at 9:34 am [Comment permalink]
@Jagadeeswaran: You were right that the sine 36° value was incorrect and so I have amended the post. (Your value for sine 36° had reversed 5 and √5, which I also fixed.)
Thanks for your inputs!
19 Nov 2014 at 6:01 pm [Comment permalink]
whats the sin6.27'?
20 Nov 2014 at 8:53 am [Comment permalink]
Do you mean the exact value of sin 6.27? This is quite a challenge - anyone like to have ago?
27 Nov 2014 at 10:33 pm [Comment permalink]
sin6°27'
Let's forget the 6° and think about 27' = (27/60)°
= (1/5)(3/4)*3°
The 1/5 means that we have to solve a quintic equation:
sin5x = 5sinx - 20sin^3x + 16sin^5x (where sin5x is known)
And that can't be done, as was shown already by Abel.
14 Mar 2015 at 7:22 am [Comment permalink]
Very interesting, thanks for sharing. Have you ever considered calculating these in terms of phi? It may produce more aesthetic solutions, and lead to general conclusions. We may be able to have mathematica (or similar) do all the work, but if not it's pretty fun to algebraically manipulate phi. If it hasn't been done, I'd be happy to work on it with you, if you're interested.
15 Mar 2015 at 4:02 pm [Comment permalink]
@Brian: Thank you for your offer. I'd be very happy if you would like to go ahead. I agree that getting Mathematica's help would be the way to go.
As mentioned a bit earlier, I know there are some errors in the current document, but I unfortunately don't have the time at the moment to dig through and correct them. If you notice any of them as you go, your suggestions for corrections would be appreciated!
30 May 2015 at 1:42 pm [Comment permalink]
Thanks for helping me with this problem. I have one more Trigonometry problem.
Problem: sin(θ+18°)=cos 60° If (0<θ<90°)
Then Find Cos5θ ?
Please Help Me!
8 Jun 2015 at 6:18 pm [Comment permalink]
Great tutorial thanx--Summarizes the whole of Trig!
13 Jul 2015 at 11:46 pm [Comment permalink]
Thanks very much for post. What about list of "exact values tan 1° to tan 90°" or "exact values cos 1° to cos 90°'? Is it existing?
1 Oct 2015 at 7:28 am [Comment permalink]
It is a good thing for students like me can you give the values from 0 to 90 of all functions????
6 Oct 2015 at 3:12 am [Comment permalink]
Great, but of course numbers involving a square root can never be "exact." The extraction of a square root is an infinite process and is never complete. The digits on the page will always be an approximation.
Prof. Norman Wildberger of the University of New South Wales has developed many other precise triangle formulas using what he calls the "spread", which is sort of a squared sine, and squared length, both easily determined from coordinates without calculating approximate square roots. They explain why comment 2 above has such simple forms. Angles are a 2,000 year old kludge for computation and their functions are most conveniently calculated now as the truncated sums of certain infinite series using radian measure, with a degree as pi/180 radians.
Professor Parent has done great work creating all these expressions using surds. Similar arduous manual methods created printed trig function tables for degrees, minutes and seconds with which humanity was stuck until electronic calculators were invented.
25 Oct 2015 at 10:42 am [Comment permalink]
We can calculate sin, cos, tan by drawing triangle, or using formulas. Is there any formula of sin(A/B)? What is the formula of sin x when x is not intenger?
25 Nov 2015 at 12:48 am [Comment permalink]
@Tim (comment-839063)
Yeah, but there's still value in keeping the "exact-but-with-irrational-terms" answer around until you know how it's going to be used. Perhaps it'll be plugged into another formula, one that itself contains a(n) irrational term(s). Maybe, in that formula, the irrational numbers will bump into each other, start discussing their issues, and realize that they can all come together to equal exactly, um, something rational... 1, let's say 1. Or 42... My point is that it's possible to use irrational numbers to calculate rational numbers.
29 Nov 2015 at 10:40 pm [Comment permalink]
[…] https://www.intmath.com/blog/mathematics/how-do-you-find-exact-values-for-the-sine-of-all-angles-6212 […]
30 Nov 2015 at 8:23 am [Comment permalink]
[…] https://www.intmath.com/blog/mathematics/how-do-you-find-exact-values-for-the-sine-of-all-angles-6212 […]
4 Dec 2015 at 3:30 am [Comment permalink]
There is another misprint.
sin(36degrees)does not equal sqrt(2sqrt(5)-10)/4.
It equals sqrt(10-2sqrt(5))/4.
24 Jan 2016 at 11:46 am [Comment permalink]
HOW TO EVALUATE BELOW EXPRESSIONS WITHOUT USING TRIGONOMETRY TABLE.
3Sin(45)^2+2Cos(60)^2
2tan60/1+tan(30)^2
24 Jan 2016 at 2:26 pm [Comment permalink]
@Abinash: This page will help: https://www.intmath.com/trigonometric-functions/3-values-trigonometric-functions.php
27 Jan 2016 at 11:53 am [Comment permalink]
can someone please tell me how to find Sin 42...I have tried everything from this post even Sin 3A leads me to Sin3*14,,now i don't know sin sin14,,,so can anyone help me!
7 Feb 2016 at 11:34 pm [Comment permalink]
My physics sir asked to find critical angle of watet-air surface that comes out to be sin inverse 2/3. Any idea how to calculate its value?
14 Mar 2016 at 8:53 am [Comment permalink]
This is no where near useful, how does sin(45degrees+30degrees)=sin45cos30+cos45+sin30 it should be sin45+sin30...
14 Mar 2016 at 9:17 am [Comment permalink]
This page gives background on this concept:
https://www.intmath.com/analytic-trigonometry/2-sum-difference-angles.php
I sympathise with you, since the math notation here is not good. See:
https://www.intmath.com/blog/learn-math/towards-more-meaningful-math-notation-661
Hope it helps.
7 May 2016 at 5:42 am [Comment permalink]
I was very interested in the problem of the representation of the trigonometric functions of angles by a finite number of combinations of the four basic arithmetic operations and the extraction of nth roots.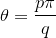
, where 
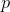and 
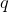are integers, then 
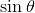can be expressed by radicals. This means, for example, that all the trigonometric functions of angles in the common trigonometric tables are always radical expressibles.
In order to answer the question of the post, It is known that, if
As an explicit example I have found, after some calculations, the exact value of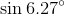
asked by Keshav ( in decimal degrees), which is
where the principal value of the roots is to be taken.
There are, of course, another number of related questions in the subject. Consider the case of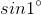
. In the expression given by Prof. Parent, the exact value is given as the sum of two irreducible cubic root of complex numbers, whose sum is a real number. In fact, 
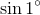cannot be expressed by real radicals, since the angle of 
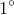is not constructible. However, this only means that 
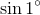cannot be expressed by a finite number of the basic operations and nth roots of real numbers, but nothing says about the possibility of representing 
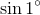by means of an infinite number of operations and root extraction of real numbers. The answer is that, if an infinite numbers of operations and extraction of roots is allowed, then 
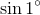can be expressed using only square roots of real numbers. But what is the explicit expression? I leave this as a challenge.
I have worked in this matter (the representation of trigonometric functions of angles by means of infinitely radicals) and I have found a lot of interesting identities. I'II give the following gift:
Where "..." means that the radical continues forever.
13 Sep 2016 at 12:14 pm [Comment permalink]
To Murray on #32-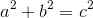
.
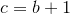
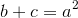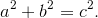
with 
:
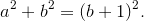
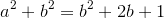
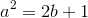
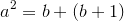
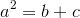
Actually, there is a reason why a 3-4-5 triangle fits the Pythagorean Theorem. If two consecutive numbers add up to the square of another number, then those three numbers are a Pythagorean Triple. It's a complicated explanation, but bear with me and we can get through this.
Let's define some variables.
Side length a
Side length b
Side length c
a < b < c
We need to find that
Let's start.
Replace
Square the (b+1):
Simplify:
Now, it is a simple matter to separate the 2b+1 into two parts:
Now, as we know, b+1=c, so:
And there you go! Now, you can find that this works for 3-4-5, 5-12-13, 7-20-21, 9-40-41, and so on.
Just something that my dad told me to in 9th grade, making me curious, so I derived it myself (I really like math).
Hope this helps!
16 Sep 2016 at 4:27 am [Comment permalink]
@Siobhan Williams I think that I can answer your question on #31. First, and question: What is the equation of the unit circle?
:
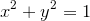
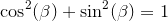
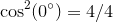
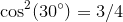
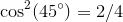
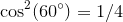
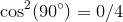
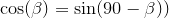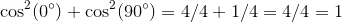
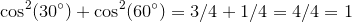
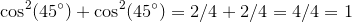
Okay. So now we can put that in terms of Theta (I'm just going to use β because I don't have a theta on this phone):
Now, you probably already knew this identity. However, from this I will derive the answer to your question.
So, let's square the different trigonometric values:
Well, I see a pattern (Remember that in Quadrant I,
And there you go. They all equal one, as they should. Hope this helps!
22 Sep 2016 at 2:42 pm [Comment permalink]
Some more “exact” values of trigonometric functions
sin 10° = (-1 + √(9 – 8*(sin 50°)))/4
sin 50° = (-1 + √(9 + 8*(sin 70°)))/4
sin 70° = (1 + √(9 - 8*(sin 10°)))/4
I know this seems a bit redundant and not quite what one is looking for – a rather quixotic quest. But they do work and they are helpful along with:
sinα±sinβ=2 sin〖1/2 (α±β)〗 cos〖1/2 (α∓β)〗
cosα+cosβ=2 cos〖1/2 (α+β)〗 cos〖1/2 (α-β)〗
22 Sep 2016 at 2:50 pm [Comment permalink]
also remember:
4*(sin 10°)*(sin 50°)*(sin 70°) = sin 30° ; (sin 10°) + (sin 50°) = (sin 70°)
AND
4* (sin 20°)*(sin 40°)*(sin 80°) = sin 60° ; sin 40° + sin 20° = sin 80°
10 Oct 2016 at 2:59 pm [Comment permalink]
The general formula could be useful:
In a few cases, this formula can help to obtain the real answer, without using complex numbers. For example, if we set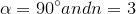
, we get
20 Dec 2016 at 1:08 pm [Comment permalink]
Here from my suggestion, I may say that the values of sin1 sin 2...... are the multiples of 0.017 bcoz if u take out the value of the sin 1 u may get 0.017 and then if u take of sin 2 u may roughly get 0.034 and so on.
20 Dec 2016 at 2:13 pm [Comment permalink]
@Vishal: This will give you good approximations only if the angles are in radians (which they are not in our case) and only for small angles.
31 Dec 2016 at 8:26 am [Comment permalink]
Notice that the values given by professor Parent can be simplified. For example:
If higher-degree radicals are allowed, then the last expression becomes much more simple:
by using DeMoivre's theorem and taking the principal values of the radicals.
17 Feb 2017 at 2:13 pm [Comment permalink]
Special angles are 0, 30, 45, 60, and 90. How I express sin20 using the ideology of these special angles?
17 Feb 2017 at 3:15 pm [Comment permalink]
Hello Olumoyegun
Did you open the PDF linked to in the article? sin 20 deg is listed on page 2.
17 Feb 2017 at 11:23 pm [Comment permalink]
Sin10°value by using identis
Sin(a+b)=sinacosb+cosasinb
Sin(a-b)=sinacosb-cosasinb
Please answer me fast
18 Feb 2017 at 8:22 am [Comment permalink]
Hello Neha
Did you open the PDF linked to in the article? sin 10 deg is listed on page 1. The methods listed in the article above are probably sufficient to derive it.
1 Mar 2017 at 11:08 am [Comment permalink]
I found a formula to find value of sinx ....
When x is 0 to 90 degree... With this you can find exact value for any angle from one formula.
6 Mar 2017 at 9:50 am [Comment permalink]
Keith Johnson says: "In Professor Parent's commentary, he works out sine 15 using the half angle formula sq root ((1 - cos 30) / 2), and shows that it simplifies to 1/2 x sq root( 2 - (sq root 3)), which he says, quite nonchalantly "or", further simplifying the expression, to 1/4 x sq root 2 x (sq root 3 - 1).
The simplification, using algebra, to go from the first expression to the second, is quite tricky. I think he may have put in the second expression without any fanfare, since both quantities are used for the value of sine 15.”
I would really like to know how we went from 1/2 x sq root( 2 - (sq root 3)) to 1/4 x sq root 2 x (sq root 3 - 1). It bothers me that I cannot understand the way the equation was simplified.
10 Mar 2017 at 12:09 pm [Comment permalink]
Would you please recheck your formula for sin 36 degrees. I get sin 36 deg = [sq. rt. (10 - 2*sq. rt. 5)]/4. The formula as you have it gives an imaginary number.
Also, I'm looking for a way to relate 2 angular measurements when their tangents are related by a non-unit constant of propotionality.
15 Mar 2017 at 5:47 pm [Comment permalink]
@Anna: Let's let
We square both sides:
Multiply the right side by 2/2:
Write that last expression as
The right-hand expression, using some recognition and insight, can be written as a square:
Multiplying that by 2/2 gives:
Taking the square root of that right hand part (and disallowing the negative case) is
QED
(That middle bit looks like magic. Actually, when figuring it out, I just started from both sides and met in the middle. Then wrote it as starting from one expression and ending with the other.)
18 Mar 2017 at 3:59 pm [Comment permalink]
@Philip: I agree with you! I fixed the typo in that formula.
As for your question, some more details (or an example) would help to indicate what you are trying to do.
5 May 2017 at 12:30 am [Comment permalink]
Instead of using 3 different formulas for sin x or cos x expressed by sin 3x or cos 3x and the imaginary unit i, depending on the quadrant of 3x, the following formulas will do for ALL angles between 0 and 90 degrees:
cosx = 1/4*(1+i*sqrt(3))(-cos3x-i*sin3x)^(1/3)
+1/4*(1-i*sqrt(3))(-cos3x+i*sin3x)^(1/3)
sinx = 1/4*(1+i*sqrt(3))(sin3x+i*cos3x)^(1/3)
+1/4*(1-i*sqrt(3))(sin3x-i*cos3x)^(1/3)
The key to these formulas are, wanting to find z^(1/3), considering the complex number -z instead of z. Then, when trying to find cos x expressed by cos 3x, sin 3x and i, one will have to consider the angle 3x - 180 . Considering 3x, this angle will lie between 180 and 270 degrees, which is outside the range -180 to 180, as required by definition. The problem will be that in the formula cos A and sin A, where A is between 180 and 270 degrees, will count as sin/cos(A-360). When dividing by 3, there will be a problem because, opposed to the case where 3x is an angle in the range from 0 to 180, 1/3*A-120 is NOT equal to 1/3*A. However, 3x-180 will always be an angle between -180 and 90. Thus the "phase displacement" will be the same for all angles from 0 to 90 degrees. Making it possible with one formula only.
Obtaining the formula for cos x first is, of course, the natural thing to do. By substituting cos x by sin (90-x) and cos 3x by sin 3(90-x), one gets an identical formula for sin x, with cos x substituted by sin x and cos 3x substituted by -sin 3x.
By the way; regarding the formulas for sin x given initially, for 3x in 1st, 2nd and 3rd quadrant, respectively; why not use +/- cos3x instead of square root signs with +/-(1-(sin3x)²). Indeed simplifies the expressions a lot.
bsh.
5 May 2017 at 12:45 am [Comment permalink]
Correction:
I wrote: "Considering 3x, this angle will lie between 180 and 270 degrees, which is outside the range -180 to 180, as required by definition."
...without making it clear that I meant for x between 60 and 90 degrees.
bsh
11 May 2017 at 11:24 pm [Comment permalink]
Simplifying formulas: Professor Parent gives us the following formula for sin x where 3x is a quadrant II-angle:
sinx = (-1/8*sin3x + 1/8*sqrt((sin3x)^2-1))^(1/3) + (-1/8*sin3x - 1/8*sqrt((sin3x)^2-1))^(1/3)
Clearly the easiest of the three to remember and use. In fact this formula applies even for sin x with 3x being a quadrant III-angle, i.e x between 60 and 90 degrees.
cosx = 1/2*(cos3x + i*sin3x)^(1/3) + 1/2*(cos3x - i*sin3x)^(1/3)
is indeed a formula valid for all x between 0 and 60 degrees. Applying it on cos(90-x) with x ranging from 30 to 90 and substituting cos(90-x) by sinx and cos/sin(3(90-x)) by -sin/cos3x gives:
sinx = 1/2*(-sin3x - i*cos3x)^(1/3) + 1/2*(-sin3x + i*cos3x)^(1/3)
Substituting i*cos3x by +/-sqrt((sin3x)^2-1) and multiplying 1/2 into the cubic root signs gives us Mr Parents formula. Valid also for cases where 3x is a quadrant III-angle.
One can even find an easier formula for the case where x is an angle in the range from 0 to 30 degrees. With the already given formula
cosx = 1/2*(cos3x + i*sin3x)^(1/3) + 1/2*(cos3x - i*sin3x)^(1/3)
in mind, one can make a small, but significant change, obtaining the following result:
i*sinx = 1/2*(cos3x + i*sin3x)^(1/3) - 1/2*(cos3x - i*sin3x)^(1/3)
Giving, by multiplying with -i on both sides:
sinx = i/2*(cos3x - i*sin3x)^(1/3) - i/2*(cos3x + i*sin3x)^(1/3)
Valid for all x between 0 and 60 degrees. By substitution this also gives us an new formula for cos x, valid for all x between 30 and 90 degrees:
cosx = i/2*(-sin3x + i*cos3x)^(1/3) - i/2*(-sin3x - i*cos3x)^(1/3)
And: Not for the sake of simplification, but to make THIS set of formulas complete:
For x between 60 and 90 degrees we have:
sinx = i/2*(-1/2-i/2*sqrt(3))*(cos3x - i*sin3x)^(1/3)
- i/2*(-1/2+i/2*sqrt(3))(cos3x + i*sin3x)^(1/3)
And for x between 0 and 30 degrees:
cosx = i/2*(-1/2-i/2*sqrt(3))*(-sin3x + i*cos3x)^(1/3)
- i/2*(-1/2+i/2*sqrt(3))(-sin3x - i*cos3x)^(1/3)
11 May 2017 at 11:35 pm [Comment permalink]
Continuing from above:
One can also find another set of formulas for sinx and cosx expressed by 3x and i, that are valid for all x between 0 and 90. By, as above, changing a sign and getting an expression for i*sinx instead of cosx, then multiplying both sides by -i. The formulas are as follows:
sinx = i/4*(1-i*sqrt(3))*(-cos3x + i*sin3x)^(1/3)
- i/4*(1+i*sqrt(3))*(-cos3x - i*sin3x)^(1/3)
cosx = i/4*(1-i*sqrt(3))*(sin3x - i*cos3x)^(1/3)
- i/4*(1+i*sqrt(3))*(sin3x + i*cos3x)^(1/3)
19 May 2017 at 5:34 pm [Comment permalink]
Even more on the same topic:
As
cos1 +/- i*sin1 = cos(90/90) +/- i*sin(90/90)
= (cos90 +/- i*sin90)^(1/90) = (+/-i)^(1/90)
one can also write:
cos1 = i^(1/90) + (-i)^(1/90)
Analogue formula for sin 1 degree:
sin1 = i^(89/90) + (-i)^(89/90) .
In general for angles between 0 and 90 degrees:
cosx = i^(x/90) + (-i)^(x/90)
and
sinx = i^((90-X)/90) + (-i)^((90-X)/90)
24 May 2017 at 7:44 pm [Comment permalink]
A bit off-topic, but at least there is a link to sin/cos 1 degree, etc, through third degree equations. And it's interesting and funny, I think.
Consider this equation:
x^3-x^2-x-1 = 0
The one and only real solution is:
x = 1/3 + 1/3*(19+3*sqrt(33))^(1/3) + 1/3*(19-3*sqrt(33))^(1/3)
Not easy to make an intelligent guess...
Now let's introduce y = 1/x . Then we'll have:
(1/y)^3-(1/y)^2-(1/y)-1 = 0
giving:
y^3+y^2+y-1 = 0
with the only solution:
y = -1/3 + 1/3*(17+3*sqrt(33))^(1/3) + 1/3*(17-3*sqrt(33))^(1/3)
x*y must, by definition, be 1, although hard to see. How can this be verified by working on the numbers only, not using the above equations as proof?
Indeed we'll have to do the multiplication which gives:
x*y = -1/9 + 1/9*(17+3*sqrt(33))^(1/3) + 1/9*(17-3*sqrt(33))^(1/3)
- 1/9*(19+3*sqrt(33))^(1/3) - 1/9*(19-3*sqrt(33))^(1/3)
+ 1/9*(26+6*sqrt(33))^(1/3) + 1/9*(26-6*sqrt(33))^(1/3)
+ 1/9*(620+108*sqrt(33))^(1/3)
+ 1/9*(620-108*sqrt(33))^(1/3) = 1
Some simplification and rearrangement:
(17+3*sqrt(33))^(1/3) + (17-3*sqrt(33))^(1/3)
- (19+3*sqrt(33))^(1/3) - (19-3*sqrt(33))^(1/3)
+ (26+6*sqrt(33))^(1/3) + (26-6*sqrt(33))^(1/3)
+ (620+108*sqrt(33))^(1/3) + (620-108*sqrt(33))^(1/3) = 10
Using a calculator gives:
(620+108*sqrt(33))^(1/3) + (620-108*sqrt(33))^(1/3) = 10
and
(620+108*sqrt(33))^(1/3) - (620-108*sqrt(33))^(1/3) = 2*sqrt(33)
With this in mind one can easily verify that
(620+/-108*sqrt(33))^(1/3) = 5 +/- sqrt(33)
Subtracting (620+108*sqrt(33))^(1/3) + (620-108*sqrt(33))^(1/3) = 10 from both sides in the above expression for x*y gives:
(17+3*sqrt(33))^(1/3) + (17-3*sqrt(33))^(1/3)
- (19+3*sqrt(33))^(1/3) - (19-3*sqrt(33))^(1/3)
+ (26+6*sqrt(33))^(1/3) + (26-6*sqrt(33))^(1/3) = 0
The remaining cubic root signs are not equally easy to handle. However, further help from the calculator gives the following result:
(17+/-3*sqrt(33))^(1/3) - (19-/+3*sqrt(33))^(1/3) +
(26-/+6*sqrt(33))^(1/3) = 0 .
According to the calculator not only the total sum, as given above, is zero, but also two partial sums. We'll try to verify this by attempting to get rid of the cubic root signs. Rearranging a little:
(26-/+6*sqrt(33))^(1/3) =
(19-/+3*sqrt(33))^(1/3) - (17+/-3*sqrt(33))^(1/3)
((26-/+6*sqrt(33))^(1/3))^3 = 26-/+6*sqrt(33)
We do the same for the expression on the right side:
((19-/+3*sqrt(33))^(1/3) - (17+/-3*sqrt(33))^(1/3))^3
= (19 -/+ 3*sqrt(33)) - 3*(-100 +/- 36*sqrt(33))^(1/3)
+ 3*(1036 +/- 180*sqrt(33))^(1/3) - (17 +/- 3*sqrt(33))
= 2 -/+ 6*sqrt(33) + 3*(100 -/+ 36*sqrt(33))^(1/3)
+ 3*(1036 +/- 180*sqrt(33))^(1/3)
Calculator gives:
(100 + 36*sqrt(33))^(1/3) + (100 - 36*sqrt(33))^(1/3) = 2
(100 + 36*sqrt(33))^(1/3) - (100 - 36*sqrt(33))^(1/3) = 2*sqrt(33)
(1036 + 180*sqrt(33))^(1/3) + (1036 - 180*sqrt(33))^(1/3) = 14
(1036 + 180*sqrt(33))^(1/3) - (1036 - 180*sqrt(33))^(1/3) = 2*sqrt(33)
...making it easy to verify that
(100 -/+ 36*sqrt(33))^(1/3) = 1 -/+ sqrt(33)
and
(1036 +/- 180*sqrt(33))^(1/3) = 7 +/- sqrt(33)
Continuing from above:
((19-/+3*sqrt(33))^(1/3) - (17+/-3*sqrt(33))^(1/3))^3
= 2 -/+ 6*sqrt(33) + 3*(100 -/+ 36*sqrt(33))^(1/3)
+ 3*(1036 +/- 180*sqrt(33))^(1/3)
= 2 -/+ 6*sqrt(33) + 3*(1 -/+ sqrt(33)) + 3*(7 +/- sqrt(33))
= 2 -/+ 6*sqrt(33) + 3 -/+ 3*sqrt(33)) + 21 +/- 3*sqrt(33))
= 26 -/+ 6*sqrt(33) .
Both sides equal. And x*y = 1 is verified.
31 May 2017 at 7:10 pm [Comment permalink]
For the sake of curiosity I made an internet search on the number
1/3 + 1/3*(19+3*sqrt(33))^(1/3) + 1/3*(19-3*sqrt(33))^(1/3) .
I found the information that this number relates to the so called "tribonacci series" in the same way as the golden ratio relates to the Fibonacci series. "Tribonacci series" being the name of the series where the elements are generated as the sum of the THREE preceding numbers instead of two, as in the Fibonacci series.
I was not surprised at all by this, as my reason for finding the above number was to find the ratio for dividing a line into THREE pieces in the same manner as the golden section. I.e.: So that the shortest part relates to the medium as the medium relates to the longest as the longest relates to the total length of the line divided. This gave the equation with the above number as the only real solution:'
x^3 - x^2 - x - 1 = 0
The website from which I got the link to the tribonacci series did not give any specific formula for the n-th element in the series. I didn't bother to check anywhere else, but was motivated to try to find a formula myself. And I managed to do so, using the same principals as for the Fibonacci series. But indeed more work.
For the Fibonacci series starting with the matrix
( 0 1 )
( 1 1 )
Is the thing to do. When doing an operation on two consecutive elements to generate a new one, the first row will be saving the last of the two while the second row will add the two. This operation will give the elements we need for the next step.
( 0 1 )( a(n-2) ) = ( a(n-1) )
( 1 1 )( a(n-1) ) ( a(n) )
Similarly for the tribonacci series we must use the matrix
( 0 1 0 )
( 0 0 1 )
( 1 1 1 )
getting
( 0 1 0 )( a(n-3) ) ( a(n-2) )
( 0 0 1 )( a(n-2) ) = ( a(n-1) )
( 1 1 1 )( a(n-1) ) ( a(n) )
The matrix for the tribonacci series has the characteristic equation
x^3 - x^2 - x - 1 = 0 . (Surprised??)
Thus l = 1/3 + 1/3*(19+3*sqrt(33))^(1/3) + 1/3*(19-3*sqrt(33))^(1/3)
is an eigenvalue for the matrix. There are also two complex, conjugated eigenvalues:
1/2*( (1-l) + i*sqrt(3l^2-2l-5)) and 1/2*( (1-l) - i*sqrt(3l^2-2l-5)) .
"l" in these expressions refers to the number l above
To find a formula, diagonalization is the keyword. Finding the inverse of the eigenvector matrix was indeed the most demanding part. But having done that, I managed to come up with this formula:
a(n) =
l^n/(3l^2-2l-1)
- (((1-l) + i*sqrt(3l^2-2l-5))^n + ((1-l) -
i*sqrt(3l^2-2l-5))^n)/((2^n)*2*(3l^2-2l-1))
- (((1-l) + i*sqrt(3l^2-2l-5))^n - ((1-l) -
i*sqrt(3l^2-2l-5))^n)*(1-3l)*i/((2^n)*2*(3l^2-2l-1)*sqrt(3l^2-2l-5))
Things like this I prefer writing by hand...
For calculation purposes, eliminating complex numbers: In the above expression we can recognize the (x + iy)^n +/- (x - iy)^n - patterns.
We get:
((1-l) + i*sqrt(3l^2-2l-5))^n + ((1-l) - i*sqrt(3l^2-2l-5))^n
= 2*(2^n*(sqrt(l^2-l-1))^n)*cos(nU)
((1-l) + i*sqrt(3l^2-2l-5))^n - ((1-l) - i*sqrt(3l^2-2l-5))^n
= 2*(2^n*(sqrt(l^2-l-1))^n)*i*sin(nU)
with the angle U defined by
cosU = (1-l)/(2(sqrt(l^2-l-1))) and
sinU = sqrt(3l^2-2l-5)/(2(sqrt(l^2-l-1)))
giving this formula:
a(n) =
l^n/(3l^2-2l-1) - (((sqrt(l^2-l-1))^n)*cos(n*u))/(3l^2-2l-1)
+ (((sqrt(l^2-l-1))^n)*(sin(n*U))*(1-3l)/((3l^2-2l-1)*sqrt(3l^2-2l-5))
Knowing the formulas above, it's not the most difficult thing to do to prove their validity by induction. Adding the complex number formulas for a(n-3), a(n-2) and a(n-1) respectively, we will get expressions like
(l^(n-3) + l^(n-2) + l^(n-1))
This can also be written: (1 + l + l^2)*l^(n-3)
But as l is a solution of x^3 - x^2 - x - 1 = 0, we can instead write
(1 + l + l^2)*l^(n-3) = l^3*l^(n-3) = l^n
The same logic applies on the (1/2*( (1-l) +/- i*sqrt(3l^2-2l-5)))^n - expressions, as these numbers are also solutions of the given equation. Substitution gives the formula for a(n) immediately.
Using the formula with cos(sin(n*U), one can also prove that lim a(n+1)/a(n) with n -> infinity is equal to l, analogue to that of the Fibonacci series.
We can write (sqrt(l^2-l-1))^n as (l^n)*(sqrt(1-1/l-1/l^2))^n .
l^n can then be isolated outside a set of brackets. As sqrt(1-1/l-1/l^2) is less than 1, (sqrt(1-1/l-1/l^2))^n will approach zero as n -> infinity, leaving both the cos- and sin-expression also to approach zero. As 1/(3l^2-2l-1) remains the same, the quotient between the expressions in brackets will approach 1. Outside the brackets we will have l^(n+1)/l^n, which is certainly equal to l. Thus lim a(n+1)/a(n) with n -> infinity is equal to l.
31 May 2017 at 7:31 pm [Comment permalink]
Above I kept referring to tribonacci/Fibonacci SERIES. I SHOULD of course have written SEQUENCES.
31 May 2017 at 7:46 pm [Comment permalink]
In fact there was also something I forgot to mention.
In the Fibonacci- as well as in the tribonacci sequences it's a matter of definition what values to set as the initial ones. I have noticed both 1,1,.. AND 0,1,... as a(1) and a(2) as starting values of the Fibonacci sequence. Maybe the most common definition of initial values of the tribonacci sequence is 0,1,1,.. , but even 0,0,1 works fine.
The preferred definition will of course have influence on the indexes used in formulas for a(n), given that we want to name the first element as a(1) and not a(0), for instance.
In my formulas, as written in the mail above, n has been chosen to define 0,1,1 as the first three elements. If wanting to have 0,0,1 as the initial values, one must replace n by (n-1) in the formulas.
However, when deducing the formula, I started with 0,0,1. The more zeros, the easier work...
8 Feb 2018 at 7:58 pm [Comment permalink]
Well Ptolemy did find the sine values of all the angles in intervals of 1/2 degrees in his work Almagest and Ulugh Beg did a table on sine values of all the angles in intervals of 1 minute. For more check this source link https://www.quora.com/How-do-I-calculate-cos-sine-etc-without-a-calculator
28 Jun 2018 at 11:06 pm [Comment permalink]
How to calculate value of sin3/5 in degree??
13 Sep 2018 at 3:53 am [Comment permalink]
Beautiful.
Totally beyond my trig skills, but still beautiful.
Thank you Professor Parent.
22 Jul 2019 at 7:46 am [Comment permalink]
A neater way for sin 42° is to express it as sin 402° = sin (330 + 72)°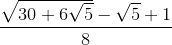
= sin 330° cos 72° + sin 72° cos 330°
End up with
30 Nov 2019 at 12:32 am [Comment permalink]
I calculated the sines of all the multiples of 3 degrees only up to 45 degrees myself, and came up with much simpler forms than the ones presented by James T. Parent.
The efficiency of the results strongly depends on the angles used in the calculation.
I also used the 'Simplify' widget from Wolfram|Alpha, and tweaked it further where possible.
Compare my result for the sine of 42 degrees with Parent's:
sin(42)=(1-sqrt(5)+sqrt(6*(5+sqrt(5))))/8
3 square roots, 2 multiplications/divisions, 3 additions/subtractions vs. 14/8/10 in Parent's solution!
I used 60-18 degrees for this.
And if you calculate sine and cosine then you only have to do that for all multiples of 3 up to 45 degrees; all other angles can be expressed as sines or cosines of angles below 45 degrees.
E.g. if 45 <= angle <= 90 then sin(angle)=cos(90-angle) and cos(angle)=sin(90-angle), etc.
The result for 18 degrees can be obtained much more easily than the complicated geometric approach to get the sine for 36 degrees.
In Parent's list, the results for 57 degrees and 87 degrees are wrong - no radicals are needed in sines of multiples of 3 degrees!
30 Nov 2019 at 9:33 am [Comment permalink]
@Herwig: Your approach sounds interesting. Would you mind sharing your results? I would add them to the article for comparison. (I'll send you my email address if you are happy to share your document.)
30 Nov 2019 at 8:02 pm [Comment permalink]
I have sent you my document ("Co(sine) of special angles."). It's written in Dutch, but the math is universal.
1 Dec 2019 at 9:43 am [Comment permalink]
@Herwig: That's great! Thanks for sharing.
I have added your document at the end of the article, as an "Alternative list".
31 Mar 2020 at 12:29 am [Comment permalink]
Hello! I'm a bit late, but I was just researching on this topic and I got to this post. I do not think that the problem is solved, since the ideal would be to have real solutions, and also those complex relationships are trivial. For example, The expression for the cosine of 10 degrees if operated is equivalent to 1/2 * [(- 1) ^ (1/18) - (- 1) ^ (17/18)], which is equivalent to 1/2 * [Cos (10 °) -iSen (10 °)
+ Cos (10 °) + iSen (10 °)], so you get to the trivial expression Cos (10 °) = Cos (10 °) that does not add value.
I believe that all expressions with complexes are trivial because they implicitly carry the expression of sines and cosines. I still haven't found someone who has calculated the cosine of 1 degree using only expressions in the reals domain.
21 Jun 2021 at 7:21 pm [Comment permalink]
@Ivan Carovano:
It can easily be shown that sin(1°) can be found from sin(3°) and solving the reduced cubic equation x^3+a1*x+a0=0 where a1=-3/4 and a0=sin(3°)/4.
There are three different real solutions {sin(-61°), sin(1°), and sin(59°)} to this equation, but it is impossible to express these without using imaginary numbers.
This is the socalled 'Casus irreducibilis' : https://en.wikipedia.org/wiki/Casus_irreducibilis
Only integer multiples of 3° can be expressed using radicals without using imaginary numbers.
30 Jul 2021 at 1:15 pm [Comment permalink]
[…] once you're done studying for the SATs and ACTs, check out all of the fun and creative ways your calculator can help you become a math […]
6 Aug 2021 at 4:54 am [Comment permalink]
[…] once you're done studying for the SATs and ACTs, check out all of the fun and creative ways your calculator can help you become a math […]
9 Sep 2021 at 9:53 pm [Comment permalink]
I solved all sines and cosines values for angles from 1° to 90°. For angles that are multiples of 3, the solutions are expressions of real number. For all angles that are not multiples of 3, the solutions are expressions of complex numbers, strictly speaking, is the sum of 2 conjugate imaginary numbers. So final values are still real numbers. In fact, the other two solutions mirror trig values of other two angles within 90° when solving the cubic equation for angles that are not multiples of 3. It's interesting one shot three birds.
5 Oct 2021 at 2:32 pm [Comment permalink]
Thank you all for your hardwork.