IntMath Newsletter: Valentine’s, applets, maps
By Murray Bourne, 14 Feb 2019
14 Feb 2019
In this Newsletter:
0. Geometry of love
1. New on IntMath: 3 new interactives
2. Quirky measurements
3. Resources: Map projections
4. Math movies: Speed of light, puzzles
5. Math puzzle: Remainders
6. Final thought: Finding your soul mate
0. Geometry of love
Happy Valentine's, everyone! Here's a mathematical interpretation of the ubiquitous symbol of love.
Did you ever consider the geometry of the idealised heart shape used in countless Valentine's messages? It's just a square rotated 45°, connected to 2 semicircles.
1. New on IntMath
(a) Math Art in Code: Animated Moore Curve
 |
This is an animation of the Moore Curve, an example of a space filling curve which consists of continuous (one-dimensional) fractal lines that bend around in ever more intricate ways such that they eventually fill a (2-dimensional) square. |
This article from the journal Nature includes an interesting application of space-filling curves to energy storage devices:
Bioinspired fractal electrodes for solar energy storages
(b) Degree and roots of polynomial equations
The concepts behind polynomial equations are quite important in mathematics, but a lot of students get bogged down in the algebra, while not seeing the big picture
 |
I rewrote the opening section and have included an interactive graph, that helps explain the concepts. |
The rest of that chapter introduces the Remainder and Factor Theorems, which I've always felt were rather useless, since only a very limited subset of polynomial equations can be solved using those techniques (the degree has to be low, and the numbers have to be "nice" so factoring is easy. But what about the huge number of cases where the numbers don't lead to easy factoring by inspection (or trial and error)?
Of course we should sove such cases using computers!
(c) Euler's Identity exploration
Leonhard Euler was a brilliant Swiss mathematician who made many contributions to the fileds of physics, astronomy and engineering.
His famous identity, eiπ + 1 = 0, has captivated people (since it neatly involves seven fundamental mathematical symbols) and proved to be very useful for simplifying many mathematical processses.
 |
This page allows you to explore the concepts behind the identity eiπ + 1 = 0. Drag the point around the circle until you achieve the identity. |
THis page was a request from reader Owen.
2. Quirky measurements
 |
Each of these seemingly informal measurements actually have a scientific component to them. |
3. Resources - map projections
(a) Map Projections on the Web
Every 2D map of the world has some distortion, the inevitable result of trying to project a 3-D object onto a 2-D plane.
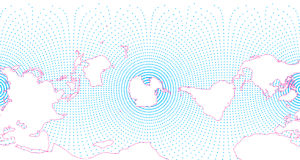
Some map types are better than others for preserving area, or shape, but none are prefect.
 |
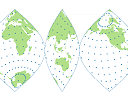GeoViz Studio has some great tools for exploring different projections. See especially the third (final) interactive example where you can choose from around 100 different projections. Go to: Map Projections on the Web |
GeoViz Studio also provides some great interfaces for creating your own map projections. See: Get Started Creating D3 Maps
These could be good starting places for students who want to learn how to code, via interesting challenges.
(b) Dymaxion Buckminster Fuller map
Inventor, architect, designer and futurist Buckminster Fuller proposed the Dymaxion projection in 1943.
Many of his designs were based on the geodesic sphere, an imaginary tesellation of a sphere into triangular pieces.
His Dymaxion Map is a projection based on the above sphere (actually basesd on an icosahedron).
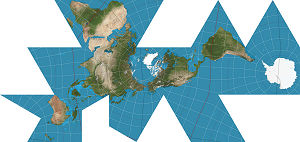
See also the results of a 2013 competition to re-invent Fuller's map:
7 Brilliant Reinventions of Buckminster Fuller's Dymaxion Map
4. Math Movies
(a) Speed of light
 |
These 3 simple NASA animations show how slow the speed of light really is, when we consider astronomical scales. This article is from Business Insider: |
(b) The joyful, perplexing world of puzzle hunts
 |
This video reminds us the human brain is wired to solve problems, and we experience a rush when we are successful, especially if it was challenging. |
One takeaway is we don't give students enough opportunity to create the problems in math class - they learn a lot by doing so!
5. Math puzzles
The puzzle in the last IntMath Newsletter asked "Who dies" in a scenario involving a rolling stone. Several conflicting answers were submitted. I added my own interpretation, which concludes D dies, but C may just have had a lucky day. Further comments are welcome!
New math puzzle: Remainders
Find the least two positive integers having the remainders 2, 3, 2 when divided by 3, 5, 7 respectively.
You can leave your response here.
6. Final thought - using math to find your soul mate?
Fewer people are meeting the love of their life in a "natural" way and are turning to apps to make connections for them. Algorithms continue to take over our lives and we all need to have a better understanding of the math behind such algorithms.
From Business Insider:
Here's how you can use math to find your soul mate — and why we're so resistant to that idea
Until next time, enjoy whatever you learn.
See the 17 Comments below.
14 Feb 2019 at 4:05 pm [Comment permalink]
Hi Murray,
Thanks again for lots of fun things to think about.
One quibble I have though is with your dismissal of the Remainder and Factor Theorems as "rather useless". On the contrary, I think they are the key to understanding how polynomials (and many other functions) "work" - even when the numbers are not "nice".
Just as one example, if you show me just one intercept of any cubic then I can factor the thing completely - and even if the intercept is not "nice" I can get a factorization of arbitrarily high accuracy on an arbitrarily large domain so long as you will let me zoom in as close as I like to read the approximate value of that intercept.
As another, if you can give me the exact value v of any polynomial, p, at any point, a, then I can reduce the problem of factoring p(x)-v to the the solution of a lower degree polynomial q where p(x)-v=(x-a)q(x).
All the best.
Alan
14 Feb 2019 at 5:34 pm [Comment permalink]
@Alan - good to hear from you, as always. My concern is with the impression given by most text books that you can solve any polynomial using the Remainder and Factor Theorems. However, you can't if the factors stray from the usual suspects: ±1, &pm2; ±3, and maybe ±0.5.
I totally agree the concept is important (whenever we can make a complex task easier by performing an interim step), but the mechanics of actually solving higher-order polynomials is always best left to the computer - either by direct solving, or by graphing and zooming in, as you mentioned.
I just feel we put students through a process (if we follow the "text book way", which many teachers do) without being totally honest about the limitations of that process, and the better alternatives.
I agree with you - the concepts are important for knowing what an equation is, and what it's solution implies. But how we get that first intercept can take students ages - and is it really "good" for them?
(I once taught a numerical computing class that involved equation solving as one of the topics. In one tutorial, while most of the students were churning away at some tedious Remainder Theorem task I had given them, one student put up his had with the correct answer which he'd obtained very quickly by trial and error. This incident challenged my view.)
14 Feb 2019 at 6:02 pm [Comment permalink]
Murray Bourne - I forwarded your ('blog?) to many friends and former colleagues with this remark: Ann and friends -
What a fascinating and joyful website! And I just sort-of stumbled into it.
Robert
I would like to comment on the article re: Using Math to Find Your Soulmate. I wish I could be brief but it is not my nature.
I have been married twice. The first was happy enough, and produced two fine sons and five (so far) grandsons. However, there was always pushing and hauling over words like 'me, mine', et c.
My background is in physics, math and statistics, with most of my career spent in signal analysis (sonar, radar, cardiac medicine). In the '70s and '80s I ran a small research group doing cardiac signal analysis for disease detection and pacemaker control. We needed an additional programmer. Of the few who applied, one had a degree in statistics from UChicago and was clearly the outstanding applicant. Our relationship progressed from boss/employee to partner in sharing and developing ideas, to friends. The partnership and deep understanding was wonderful. I often asked myself why a marriage couldn't have a partnership like that.
Eventually, I left the company and took a job out of state. It soon became clear that my then-wife and family had no intention of joining me. During that first year, several friends from my former company came to visit me and see how I was doing - including my former partner. This was some eight years after we met. Eight years and one minute after we met, we fell in love. Up to that point we had never laid romantic eyes on each other.
My first wife and I agreed to divorce. I re-married about a year later to my partner and statistic major. We have now been married 30 years and counting. Our underlying theme is P.F.L. (Partners, Friends and Lovers), like Andrew Carnegie's three legged stool, the supporting structure for our entire relationship.
And all because of statistics.
14 Feb 2019 at 6:55 pm [Comment permalink]
I'm sorry, Dave. I'm afraid I can't do that.
Something messed up. :-(