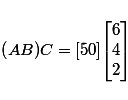Archive for the ‘Mathematics’ Category

The fascinating Map to Multiplication may not be all it seems, notwithstanding its cleverness.

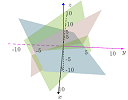
This 3D planes applet allows you to explore the concept of geometrically solving 3 equations in 3 unknowns.

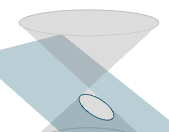
This interactive applet allows you to explore the concept of slicing a cone by a plane at various angles and positions, resulting in conic sections.

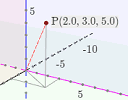
I recently added a 3D interactive graph which you can use to explore the x-, y- and z-axis system.

Here's a numerical solution to an earlier problem we discussed involving a roller door.

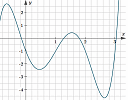
A quintic curve is a polynomial of degree 5. Given such a curve, how do you work backwards to find the original function expression?

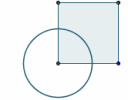
Here's a reader's approach to the age old problem of finding a square with the same area as a given circle, called "squaring the circle"

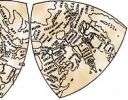
The butterfly map of the world is based on Reuleaux triangles. This article explores some of the story behind this interesting map.

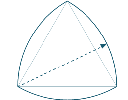
Reuleaux triangles have a property similar to circles - they have constant diameter when rotated.

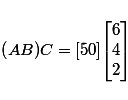
A 1×1 matrix is often regarded as a scalar quantity, but is that correct? This article explores a reader's question.