Roller Door Problem and Polymath Software

Some time ago I wrote an article about a roller door problem. A reader needed a formula so he could easily work out the number of turns of a roller door for different height doors.
I presented 3 different models for solving the problem, all of which gave pretty good results.
A while later, I heard from Michael Cutlip, developer of Polymath Software. Polymath uses numerical approaches for problem solving. According to the site, the professional version can cope with:

• Linear Equations - up to 264 simultaneous equations
• Nonlinear Equations - up to 300 simultaneous nonlinear and 300 additional explicit algebraic equations
• Differential Equations - up to 300 simultaneous ordinary differential and 300 additional explicit algebraic equations
• Data analysis and Regression - up to 200 variables with up to 1000 data points for each, with capabilities for linear, multiple linear, and nonlinear regressions with extensive statistics plus polynomial and spline fitting with interpolation and graphing capabilities

Being numerical in approach, Polymath can export solutions to Excel for further analysis, or graphing. There is some integration with Matlab, too.
I had a play with Polymath, and I feel it is an interesting tool for numerical solutions to various problems. It's quite easy to set up problems and there are many example ones to get you going. There's a short free trial period.
As Michael rightly says:

My approach to general problem solving is to use numerical methods that are easily available within Polymath Software. My feeling is that real world problems are solved with numerical methods, and thus students and their teachers should utilize these techniques while math is being taught. Perhaps this is because I am a retired engineering professor and have been working in this area since about 1980. The application of numerical methods can make math much easier and much more fun...

Roller Door Problem Solution with Numerical Methods

Michael worked on the roller door problem using Polymath Software and provided some more solutions.

Michael B. Cutlip
Emeritus Professor of Chemical Engineering
University of Connecticut, Storrs, CT 06269-3222

This solution utilizes numerical analysis problem solving capabilities such as are available in the easy-to-use Polymath Software.

The problem is detailed in the article Roller Door Problem, which contains some solutions.

Michael's Solution using Polymath

Problem 1: Given L, Determine n

The objective of the problem is to be able to design a spring system for a garage roller door to determine the number of turns for the door for the starting radius and the gap between spirals.

The length of the door is given by

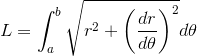
where

r = x + yθ

x = starting radius (x = 127.5)

y = gap/(2π) where gap is known (gap = 4)

a = 0

b = θ = 2πn (where n = turns) so n = θ /2π

Thus

Writing the above integral equation as an ordinary differential equation (using Polymath notation) gives

d(L)/d(theta) =sqrt((x+y*theta)^2+y^2) (1)

Equation (1) can be used for a desired length *Ldesired” when the gap and x values are known. The initial condition for the differential equation is

L = 0 when θ = 0

Thus a numerical solution can determine the theta corresponding to this Ldesired value.

Since n = q /(2*pi), one can differentiate with respect to q, and the following differential equation can be used to calculate n

d(n) / d(theta) = 1/(2*pi) (2)

with initial condition of n = 0 at θ = 0.

The simultaneous numerical integration of differential equations (1) and (2) to the value of theta where L = Ldesired will give the calculated value of n that is the number of turns.

The Switch variable will be used to hold both L and n at the desired value of Ldesired by setting both derivatives equal to zero.

POLYMATH PROGRAM LISTING

# Roller Door Problem Parameters

x = 127.5
gap = 4
y = gap/(2*pi)
pi=3.1416
Ldesired = 2000

# Logic to hold integration when L= Ldesired yielding number of turns n.

# The Switch defined below is used to hold integrations of L and n at final conditions

Switch= If (L < Ldesired) Then (1) Else (0)

# Ordinary differential equations giving L and n

d(L) / d(theta) = Switch*sqrt((x+y*theta)^2+y^2)
n(0) = 0
L(0) = 0
d(n) / d(theta) = Switch/(2*pi)
theta(0) = 0
theta(f) = 20 # This value must be large enough to allow Ldesired to be attained (Switch becomes 0) during solution.

POLYMATH Report

Ordinary Differential Equations

Calculated values of DEQ variables

The answer is highlighted in red.

Differential equations

1	d(L)/d(theta) = Switch*sqrt((x+y*theta)^2+y^2)
2	d(n)/d(theta) = Switch/(2*pi)

Explicit equations

1	x = 127.5
2	gap = 4
3	pi = 3.1416
4	y = gap/(2*pi)
5	Ldesired = 2000
6	Switch = If (L < Ldesired) Then (1) Else (0)

General

Total number of equations	8
Number of differential equations	2
Number of explicit equations	6
Elapsed time	0.000 sec
Solution method	RKF_45
Step size guess. h	0.000001
Truncation error tolerance. eps	0.000001

Problem 2: Given n, Determine L

The objective of the problem is to be able to design a spring system for a garage roller door to determine the number of turns for the door for the starting radius, the gap between spirals and the length of the door.

The simultaneous numerical integration of differential equations (1) and (2) to the value of theta where n = ndesired will give the calculated value of the door length L.

The Switch variable will be used to hold both L and n at the desired value of ndesired by setting both derivatives equal to zero.

POLYMATH PROGRAM LISTING

# Roller Door Problem Parameters

x=127.5

gap=4

y=gap/(2*pi)

pi=3.1416

ndesired = 2

# Logic to hold integration when n = ndesired yielding door length
L The Switch defined below is used to hold integrations of L and
n at final conditions

Switch= If ( n < ndesired) Then (1) Else (0)

# Ordinary differential equations giving L and n

d(L) / d(theta) = Switch*sqrt((x+y*theta)^2+y^2)

n(0) = 0

L(0) = 0

d(n) / d(theta) = Switch/(2*pi)

theta(0) = 0

theta(f) = 20

# This last value must be large enough to allow ndesired to be attained (Switch
becomes 0) during solution.

POLYMATH Report

Roller Door Problem - Given n, Calculate L

Ordinary Differential Equations

Calculated values of DEQ variables

Differential equations

1. d(L)/d(theta) = Switch*sqrt((x+y*theta)^2+y^2)

2. d(n)/d(theta) = Switch/(2*pi)

Explicit equations

1	x = 127.5
2	gap = 4
3	pi = 3.1416
4	y = gap/(2*pi)
5	ndesired = 2
6	Switch = If ( n < ndesired) Then (1) Else (0)

General

Total number of equations	8
Number of differential equations	2
Number of explicit equations	6
Elapsed time	0.000 sec
Solution method	RKF_45
Step size guess. h	0.000001
Truncation error tolerance. eps	0.000001

Conclusion

Thank you Michael for your numerical solutions! This is quite a neat way to solve this problem.

Be the first to comment below.