Understanding Cylindrical Coordinates in Geometry

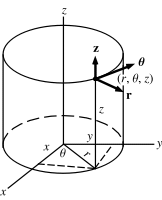
What are Cylindrical Coordinates?

The first number, r, is the distance from the origin, which is the point (0, 0, 0) in space. The second number, ?, is the angle from the z-axis in the xy-plane. The third number, z, is the height from the xy-plane.

Using Cylindrical Coordinates to Describe Vector Fields

Cylindrical coordinates can be used to describe vector fields, which are mathematical objects that can be used to describe the direction and magnitude of forces in physical systems. Vector fields are described using cylindrical coordinates by using three equations; one for each coordinate. The equations used to describe vector fields in cylindrical coordinates are as follows:

• F_r = (r, ?, z) * (cos ?, sin ?, 0)
• F_? = (r, ?, z) * ( -sin ?, cos ?, 0)
• F_z = (r, ?, z) * (0, 0, 1)

These equations are used to calculate the components of a vector field in cylindrical coordinates.

Cylindrical Surfaces and Cylindrical Graphs

Cylindrical coordinates can also be used to describe cylindrical surfaces and cylindrical graphs. Cylindrical surfaces are surfaces described by equations of the form z = f(r, ?). Cylindrical graphs are graphs of functions of the form z = f(r, ?). Both of these types of surfaces and graphs can be used to visualize and analyze data in three-dimensional space.

Practice Problems

Let�s try some practice problems to test our understanding of cylindrical coordinates.

1. What is the equation for a cylindrical surface?
   The equation for a cylindrical surface is z = f(r, ?).
2. What are the three equations used to describe vector fields in cylindrical coordinates?
   The three equations used to describe vector fields in cylindrical coordinates are: F_r = (r, ?, z) * (cos ?, sin ?, 0), F_? = (r, ?, z) * ( -sin ?, cos ?, 0), and F_z = (r, ?, z) * (0, 0, 1).
3. What is the point (0, 0, 0) in space referred to as?
   The point (0, 0, 0) in space is referred to as the origin.
4. What is the angle from the z-axis in the xy-plane referred to as?
   The angle from the z-axis in the xy-plane is referred to as ?.
5. What is the height from the xy-plane referred to as?
   The height from the xy-plane is referred to as z.
6. What kind of graphs can be used to visualize and analyze data in three-dimensional space?
   Cylindrical graphs of functions of the form z = f(r, ?) can be used to visualize and analyze data in three-dimensional space.

Summary

Cylindrical coordinates are an important concept in geometry, and are used to describe points in three-dimensional space. The three coordinates are referred to as r, ?, and z, and they represent the distance from the origin, the angle from the z-axis in the xy-plane, and the height from the xy-plane, respectively. Cylindrical coordinates can be used to describe vector fields and cylindrical surfaces and graphs. By understanding cylindrical coordinates, we can better understand and visualize data in three-dimensional space.

FAQ

What is the formula for the conversion between cylindrical and Cartesian coordinates?

The formula for the conversion between cylindrical and Cartesian coordinates is: x = rcos?, y = rsin?, z = z.

What are the three coordinates in cylindrical coordinates?

The three coordinates in cylindrical coordinates are the radial distance (r), the angle (?), and the height (z).

What are the advantages of using cylindrical coordinates?

The advantages of using cylindrical coordinates include the ability to easily represent 3-dimensional objects in a 2-dimensional plane, the ability to describe curved surfaces, and the ability to simplify calculations. Cylindrical coordinates are also useful for representing motion in a vertical plane, such as a projectile motion.